1. 向量究竟是什么
视频
Youtube
二维向量的乘法:
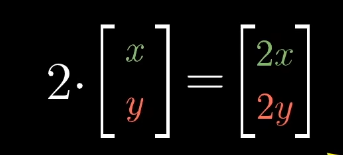
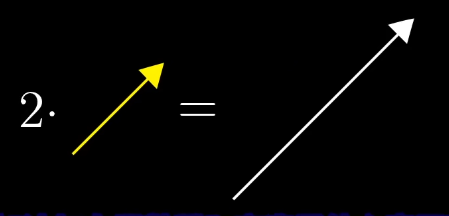
二维向量的加法:


2. 线性组合、张成的空间与基
视频
单位向量,用字母 + hat 来表示

通过改变所选择的标量,可以得到任何的二维向量:

如果只让其中一个标量变化,会画出两条相交的直线:

但是如果两个单位向量重叠,产生的新向量始终在一条线上:
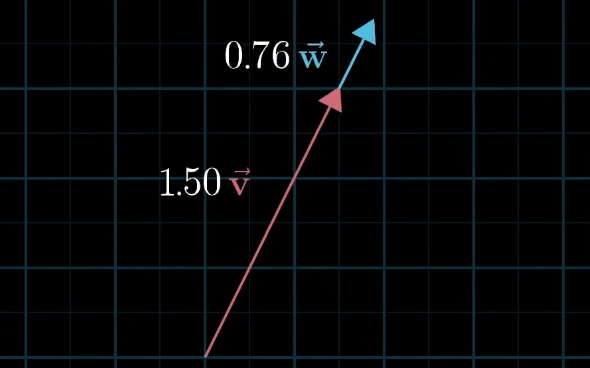
如果两个单位向量的长度为 0,也只能乖乖呆在原点。
所有可以表示为给定向量线性组合的向量集合,被称为给定向量“张成的空间”(span)。
对于三维向量来说, 两个向量张成的空间就是他们所有可能的线性组合,也就是缩放再相加之后所有可能得到的向量。最终会是一个平面:
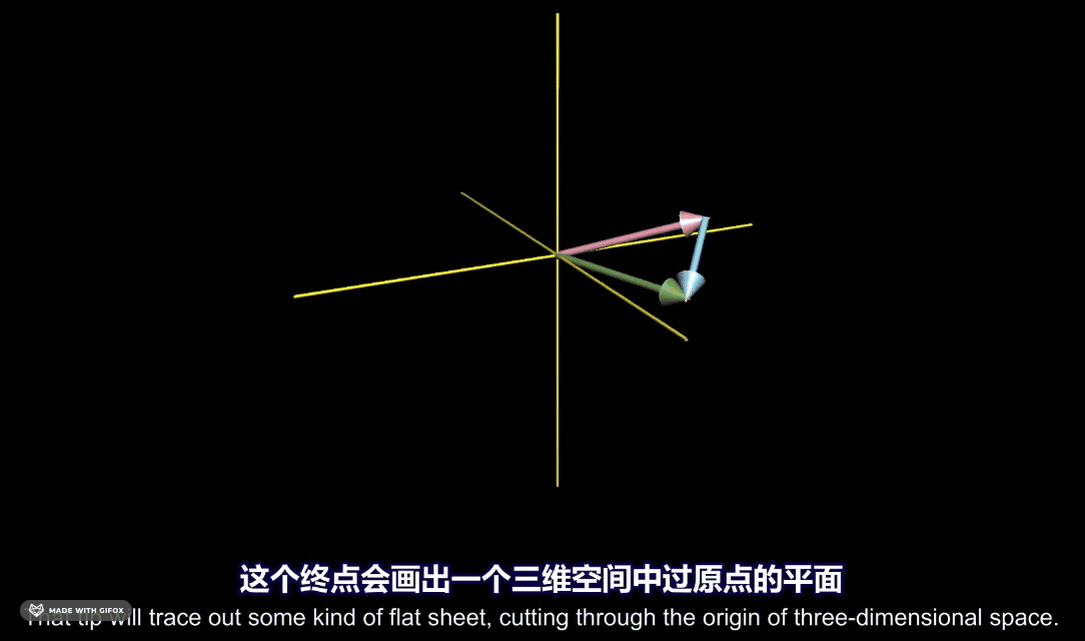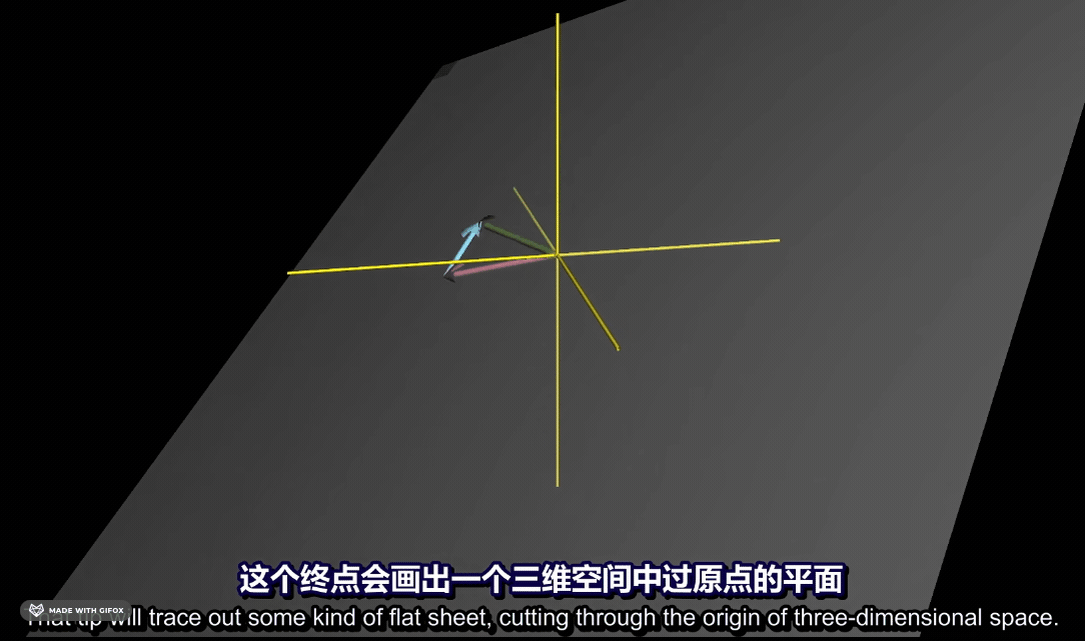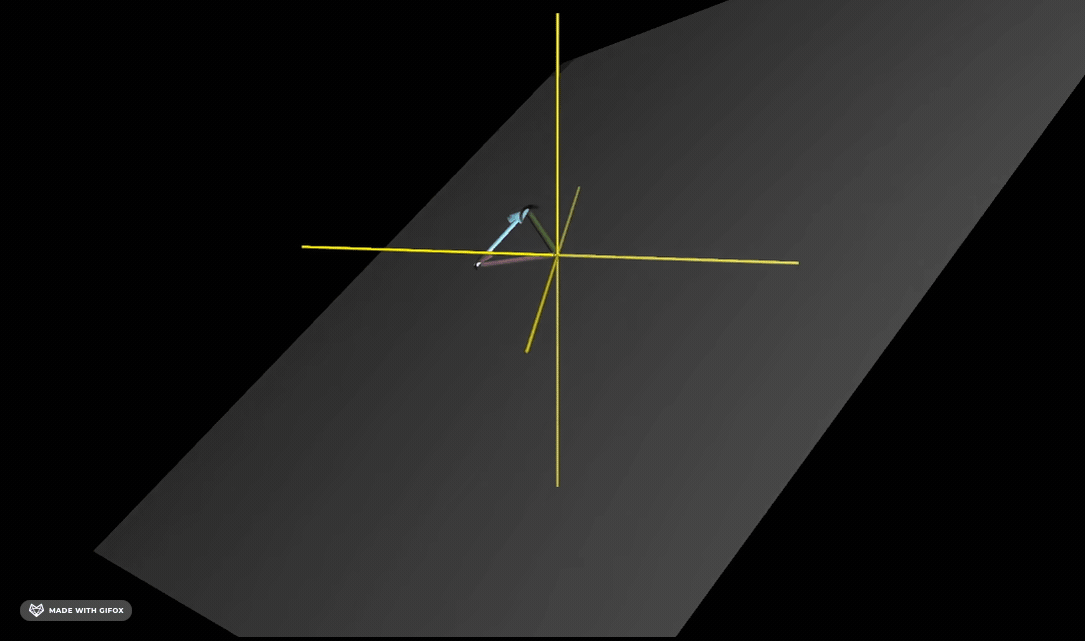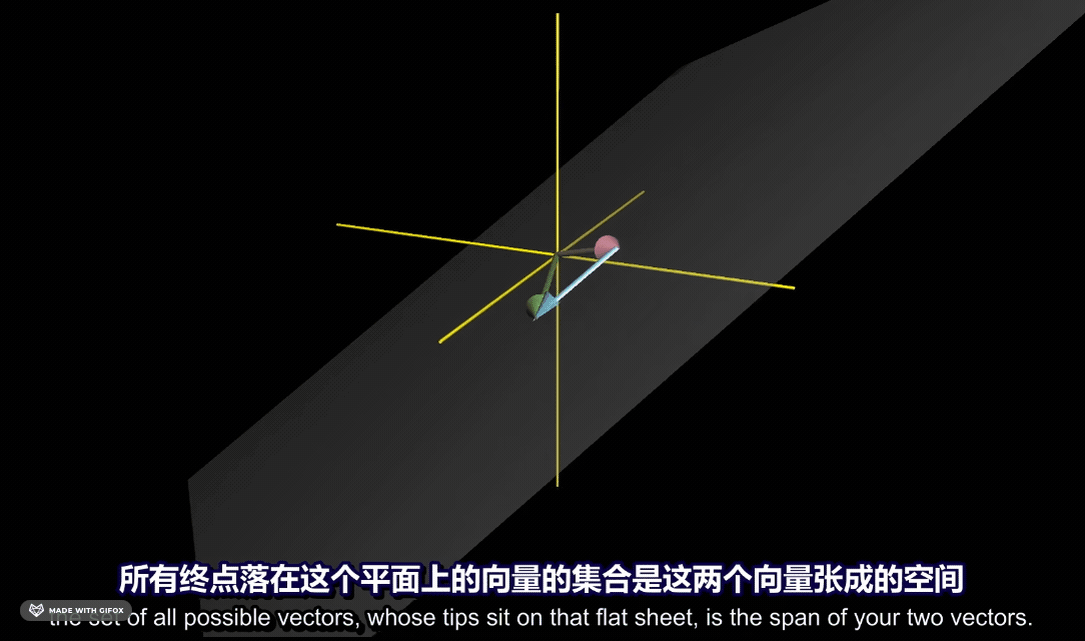
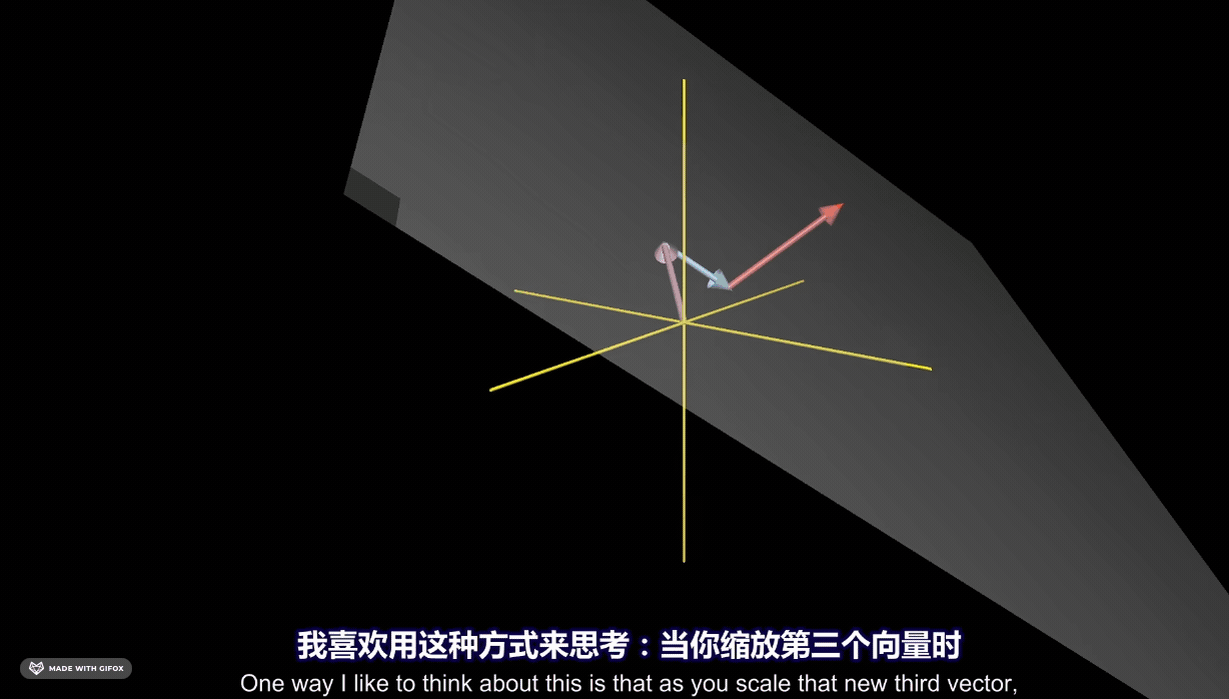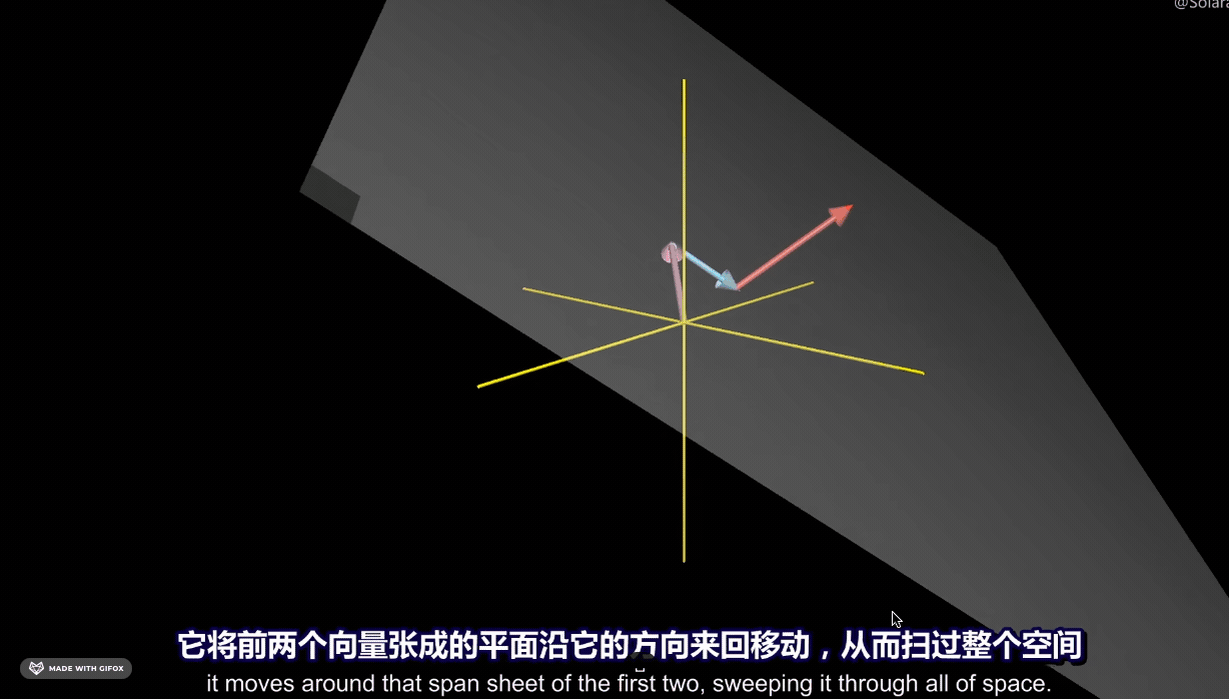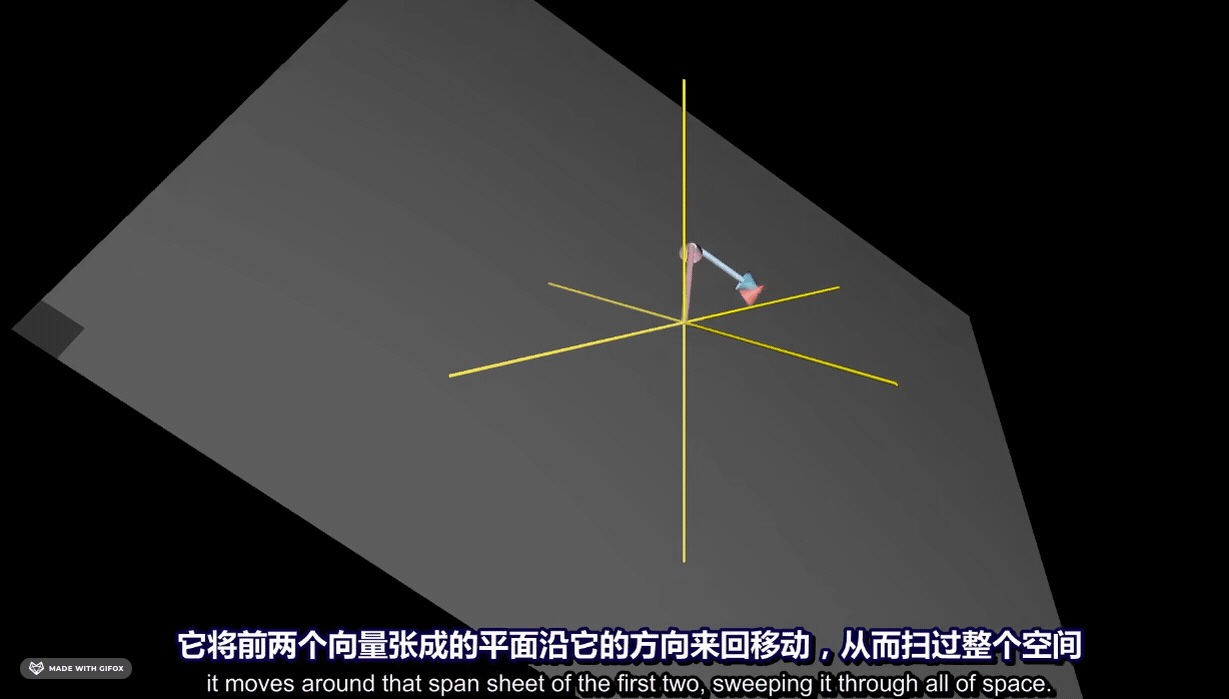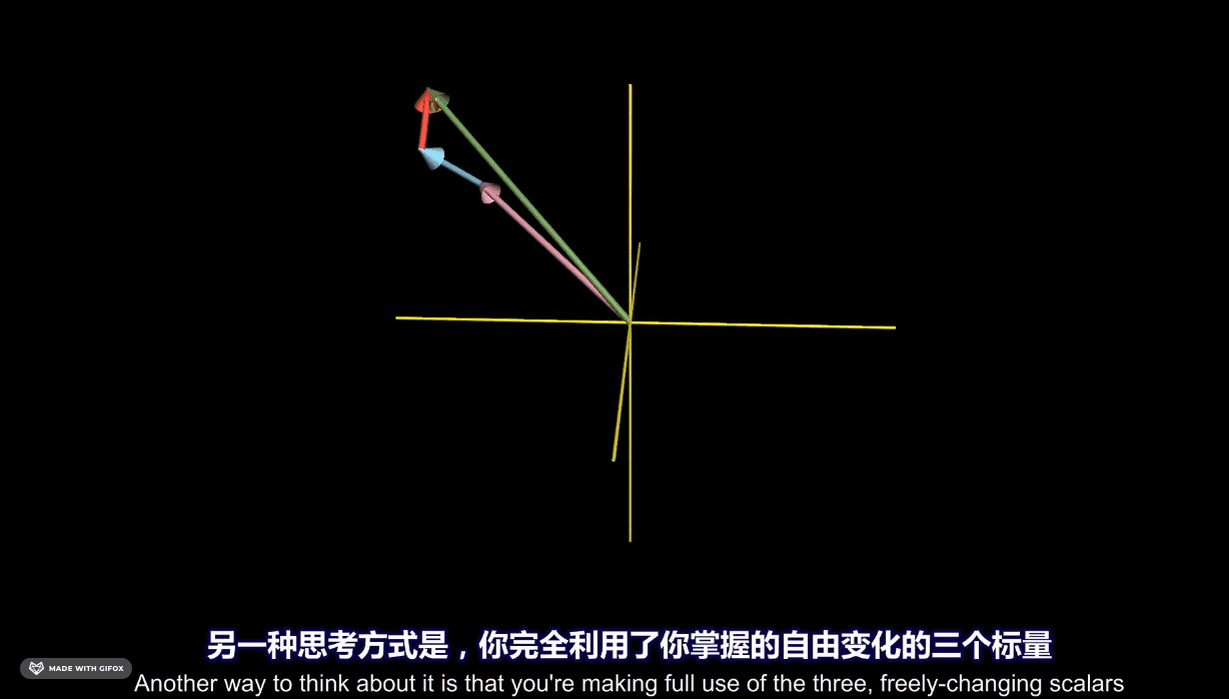
三个向量的张成空间可以得到空间中所有的三维向量: