1. 什么是动态规划

动态规划（英语：Dynamic programming，简称DP），是一种通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法，动态规划常常适用于有重叠子问题和最优子结构性质的问题，动态规划方法所耗时间往往远少于朴素解法。动态规划背后的基本思想非常简单，大致上，若要解一个给定问题，我们需要解其不同部分（即子问题），再根据子问题的解以得出原问题的解。

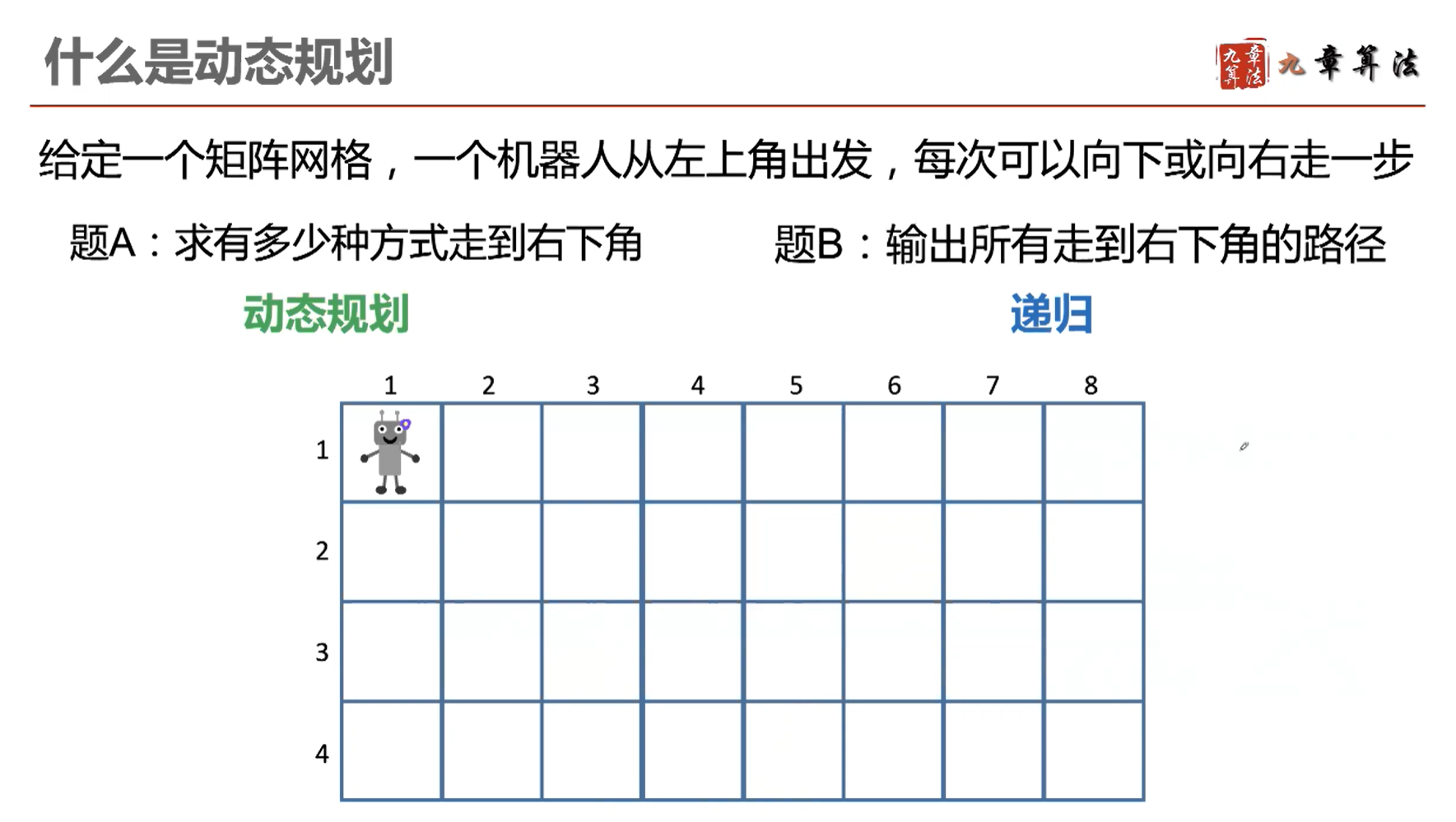
再题目上，动态规划通常有以下特点：

1. 计数
   • 有多少方式走到右下角
   • 有多少种方法选出 k 个数使得和是sum
2. 求最大值最小值
   • 从左上角走到右下角路径的最大数字和
   • 最长上升子序列长度
3. 求存在性
   • 取石子游戏，先手是否必胜
   • 能不能需拿出 k 个数使得和是 Sum

2. 例题

2.1 零钱兑换

题目：

leetcode来源

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。

你可以认为每种硬币的数量是无限的。

分析：

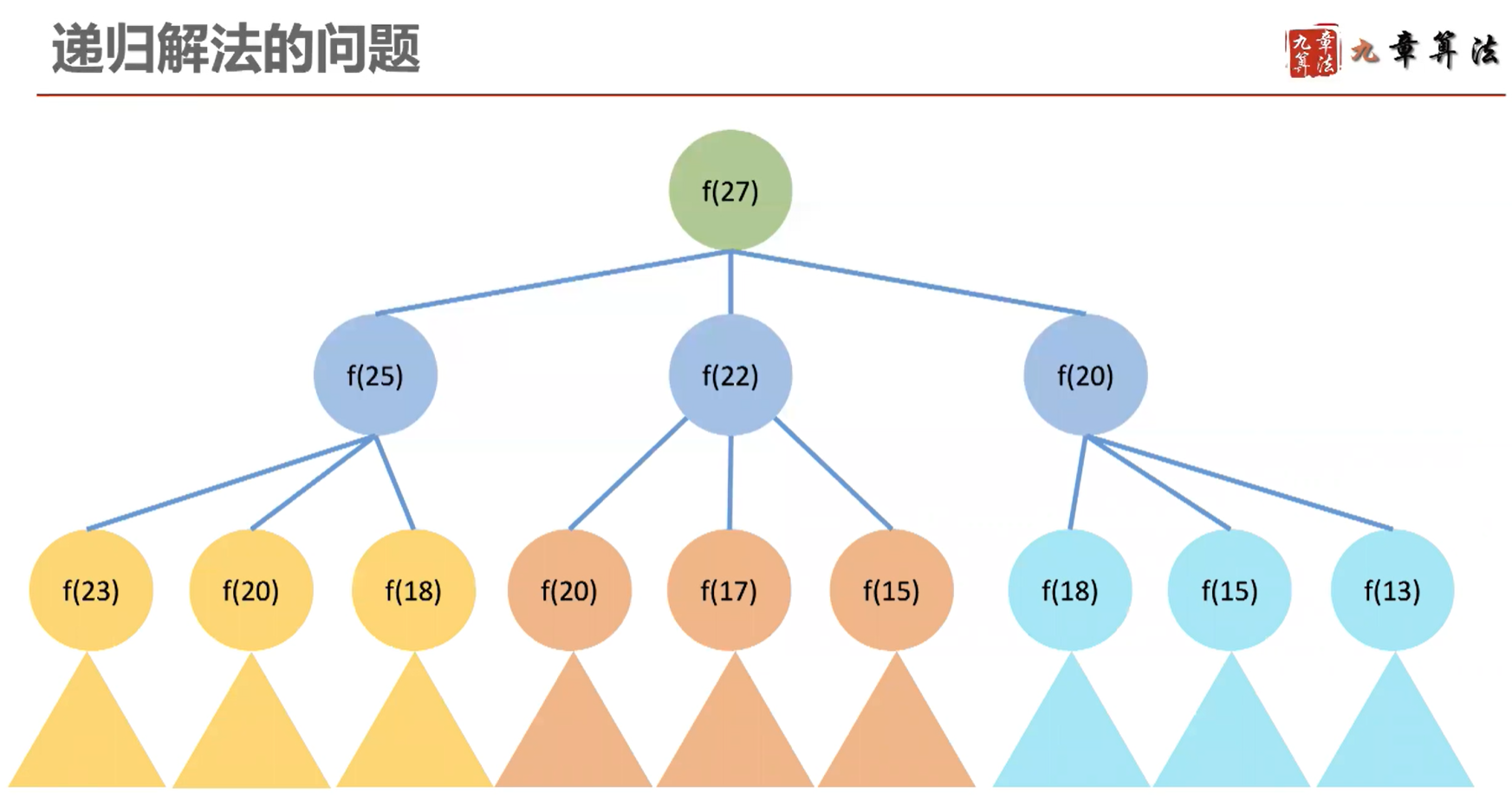
假设我们有硬币 3、5、7，需要凑成 27 元：

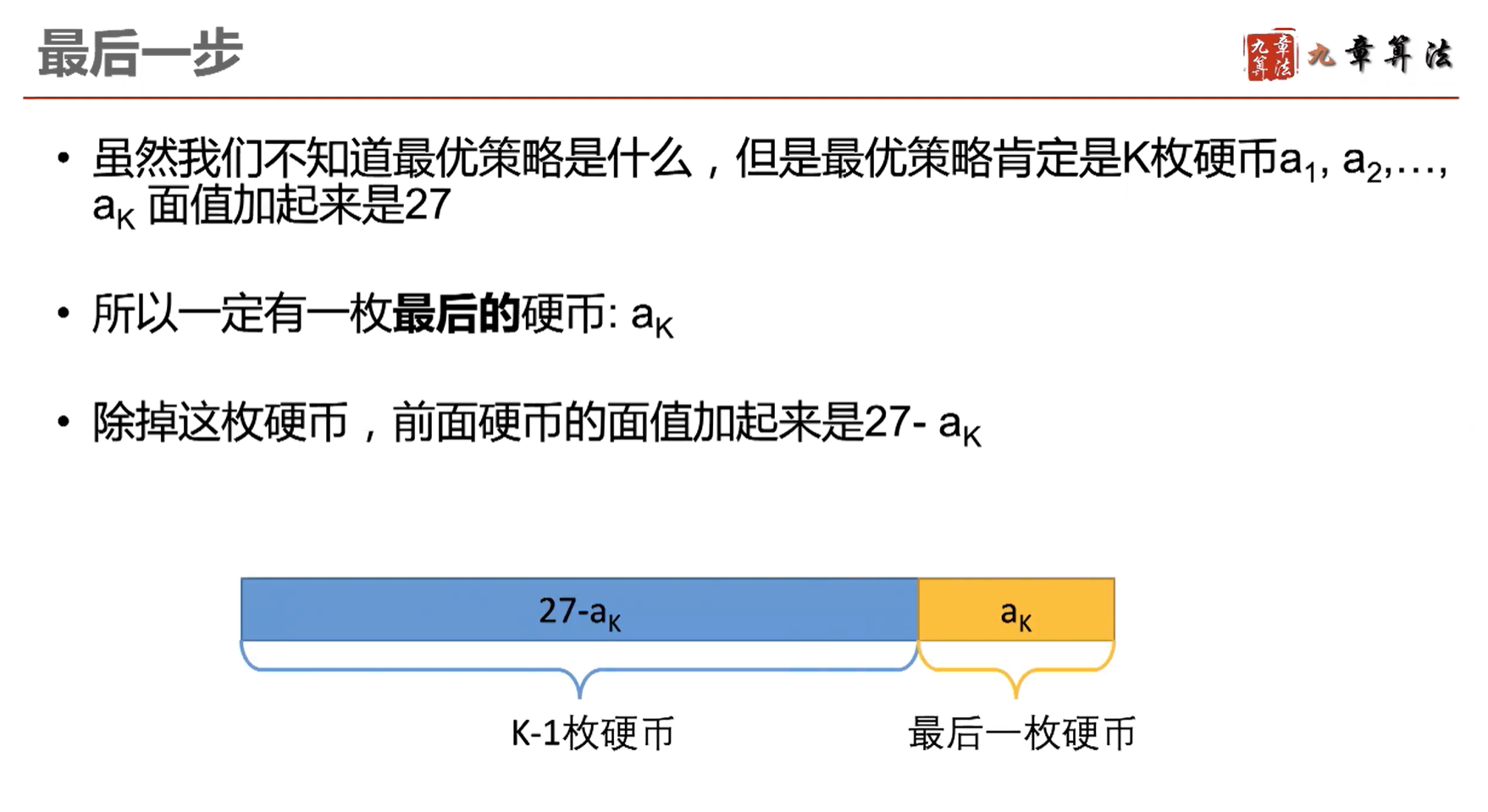
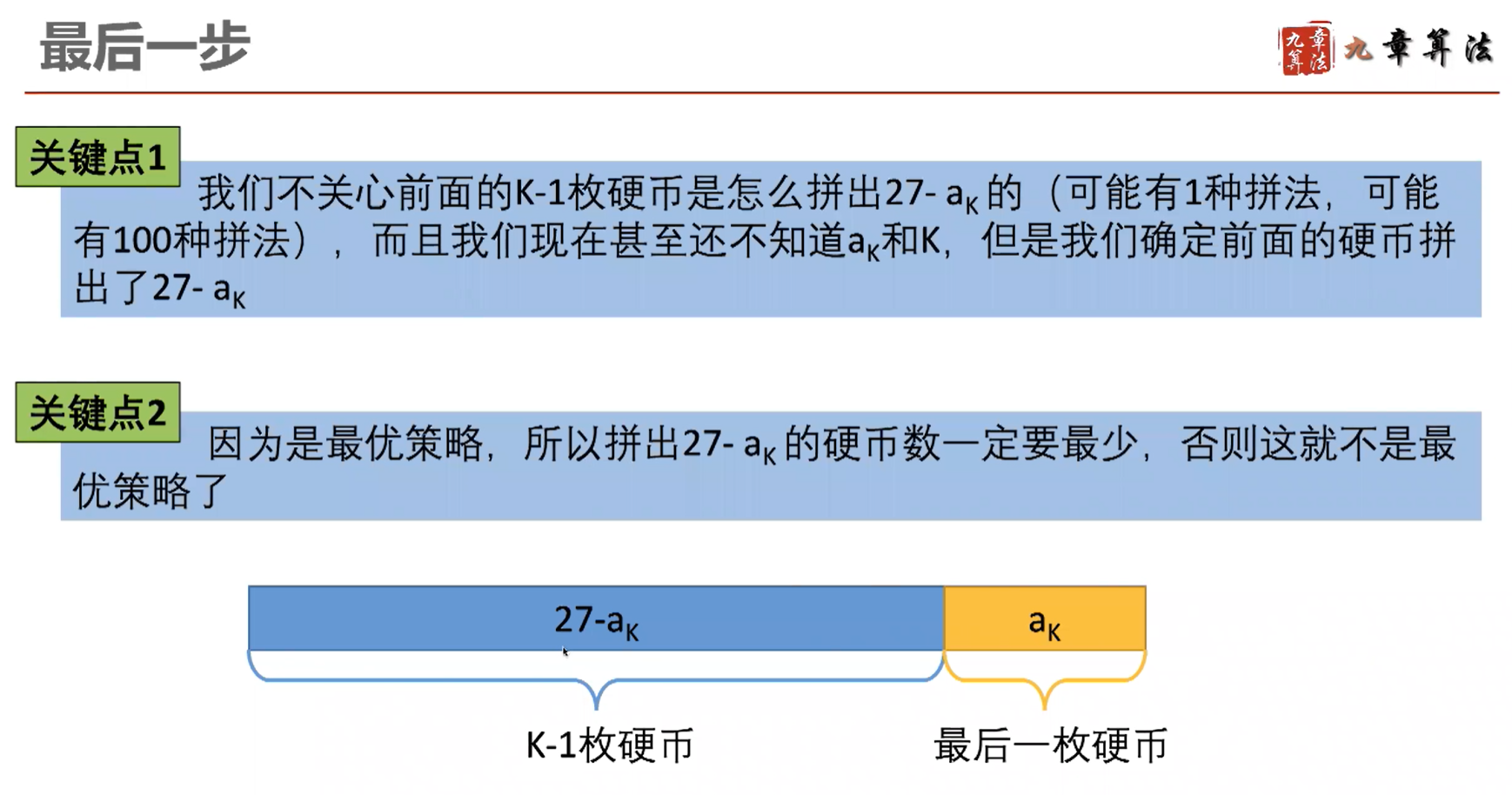
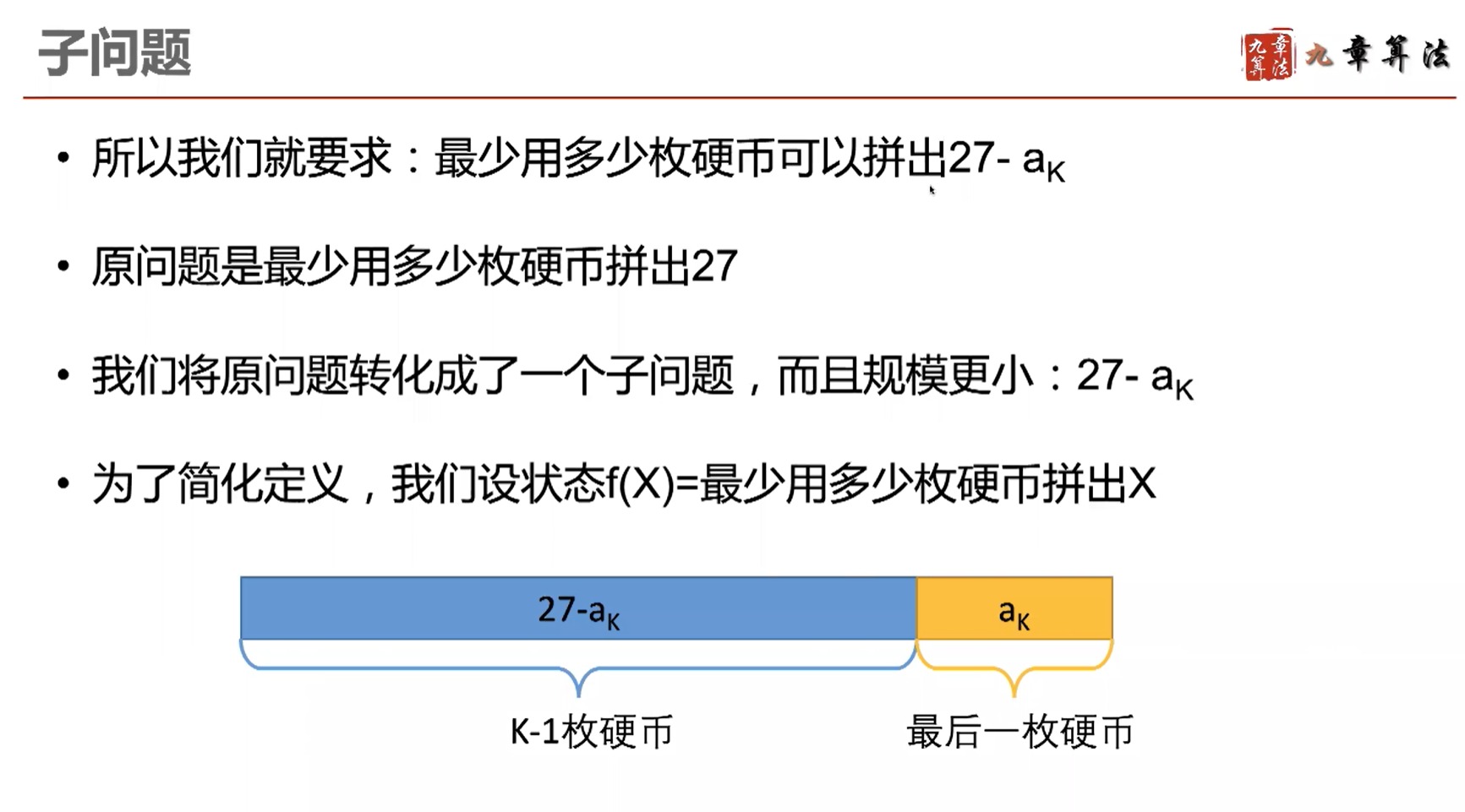
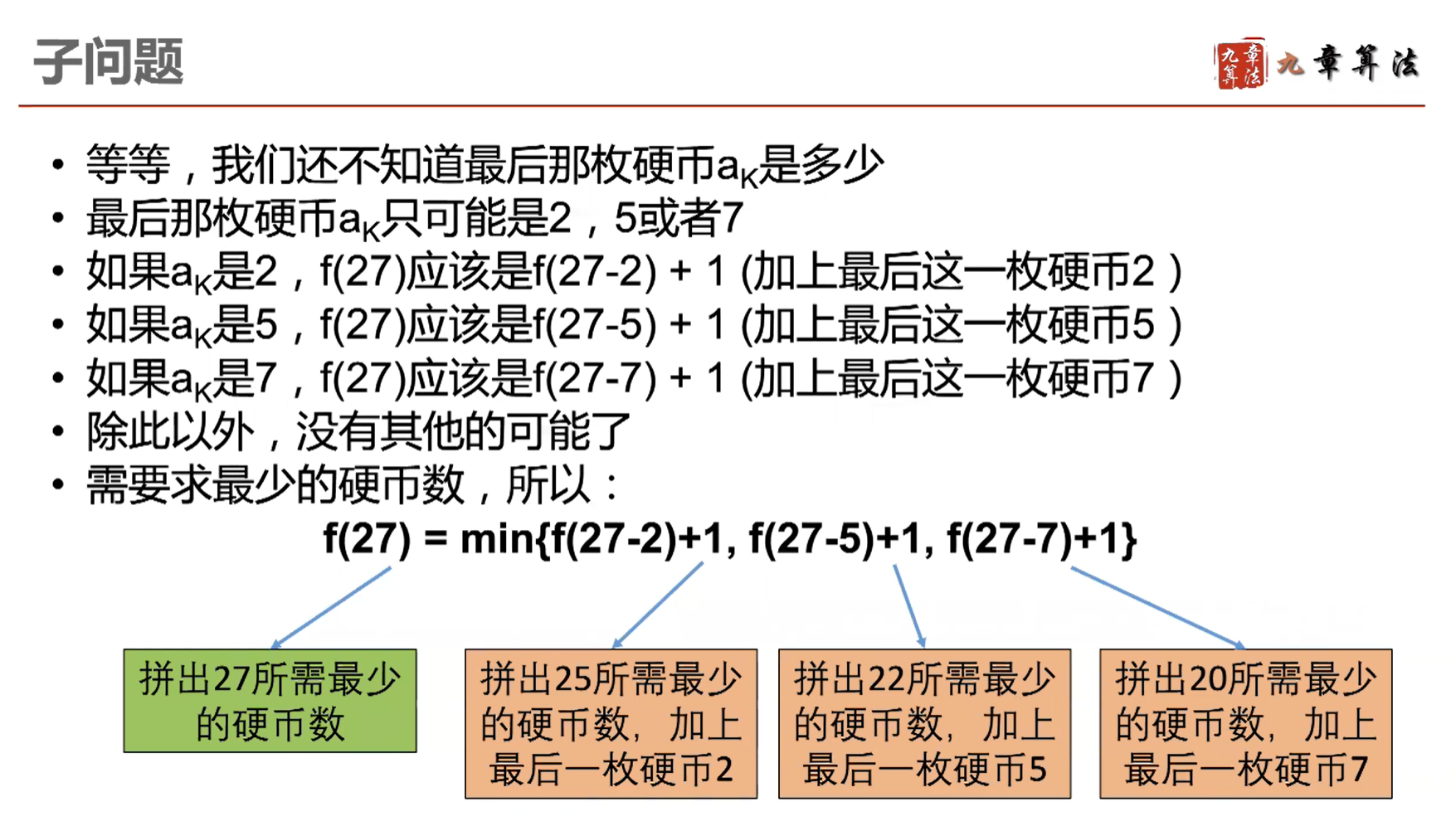
将上面的思路转为递归算法，可以写为：

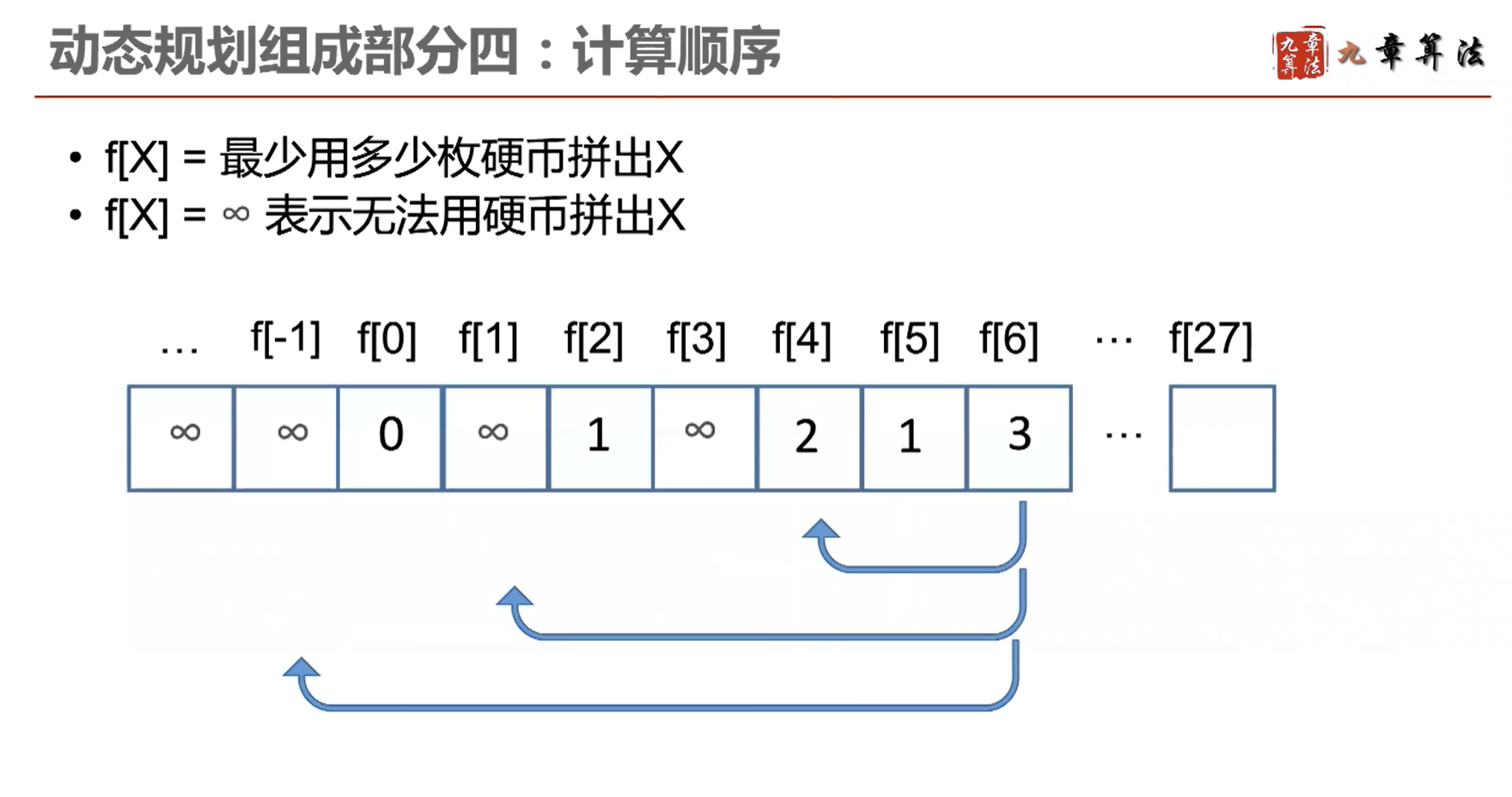
为了优化算法，我们可以将每一个计算出来的 f(x) 存储起来，依次从 f(0) 求到 f(x)，这样就可以简化重复的计算：

解答：

// coins = [3, 5, 7]
// f(x) = 最少用多少枚硬币拼出x
// f(x) = min{f(x-3)+1, f(x-5)+1, f(x-7)+1} 

function coinChange(coins: number[], amount: number): number {
    const dp: number[] = []
    dp[0] = 0
    for (let i = 1; i <= amount; i++) {
        dp[i] = Math.min(...coins.reduce((acc: number[], current) => {
            if (dp[i - current] !== undefined) {
                return [...acc, dp[i - current] + 1]
            } else {
                return acc
            }
        }, []))
    }
    if (dp[amount] === Infinity) {
        return -1
    } else {
        return dp[amount]
    }
};